当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
ワーカー(就業者)のストレス→ストレス指数参照.
ワーカー(就業者)の快適性評価→オフィス評価のシミュレーション参照.
ワードの検索(用語検索)→文章意味集計(用語検索)システム(「J−03」 参照.プログラムは「M−20」.)
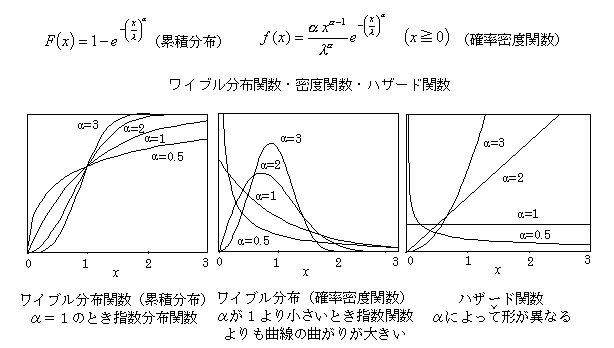
ワイブル分布(Weibull distribution)以下の式でlとλは同じ定数を表わします.
ワイブル累積関数において,a=1のときが,累積指数分布関数になるので,指数分布はワイブル分布の特別な場合になる.指数分布において確率変数をベキ変換した場合であると言える。べき指数があるので2回の対数変換をすることによって、確率変数と直線的な関係として把握できる。この点はは2重指数分布(ガンベル分布)と似ているが、ガンベル分布が指数関数・指数関数であるのに対して、ワイブル分布はベキ関数・指数関数であり、意味が異なっている。応用的なモデル構成の場合、対数線形モデル(ポアソン分布)が出現度数の対数値、ロジット(対数オッズ)が該当・非該当(当たり・はずれ)の対数値の差に関連するが、指数分布とワイブル分布は、非該当の数のみに依存依存する現象と関連するので、その考え方がハザード関数(生存に対する一定割合の考え方)と一致する。したがって、指数分布やワイブル分布はハザード関数と単純に結びつく。ワイブル分布は、指数分布(残りの一定割合が変化するというモデルの表現)の要因変数に圧縮や増幅などのバネ規制や加速度などの別の機能を付加したものと考えることができるので、ベキ指数(加速度など)の大きさによって、現象的に異なったハザード関数が構成される。(2005.2)

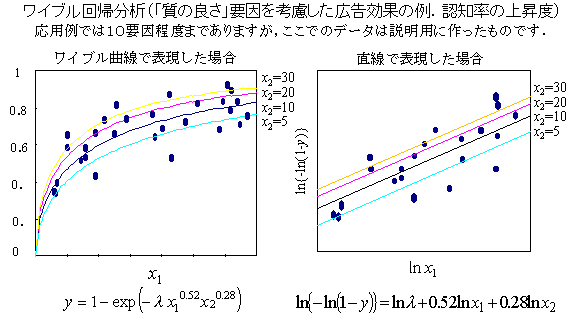
ワイブル回帰分析 以下の式でlとλは同じ定数を表わします.
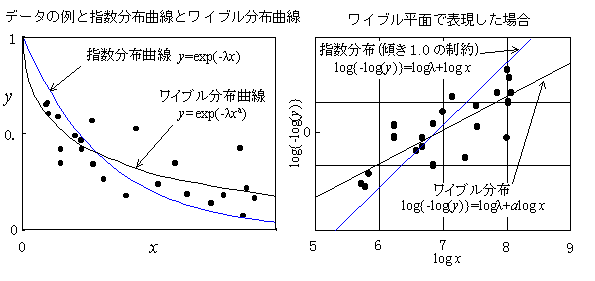
指数分布の累積確率分布関数(学習曲線)が,y=1-exp(-lx) (x≧0,lは定数)のように表現したとき,変数xがベキ形式になると,y=1-exp(-lxa)(x≧0,a,l定数)のように表現でき,ワイブル分布の累積確率分布関数になる.ワイブル累積関数において,a=1のときが,累積指数分布関数になるので,指数分布はワイブル分布の特別な場合になる.ワイブル分布関数は,パラメータが1つ多いので,指数分布関数より,一般に,データに良く当てはまる.図にあるように,実際のデータを見てみると,ワイブルの直線平面では,指数分布関数は,傾きが1.0になるという制約があるので,データに当てはまりにくい.指数分布は,一定期間での学習割合速度(波及割合速度)が一定であるという便利な特徴があるが(未遡及者の一定割合に遡及していくというモデル),データには必ずしも適合しない.
ワイブル分布のパラメータ(a)は,1.0より小さくなることが多いが,このことは,初期の効率が良いが,後の方では,非遡及者がすくなるなることに加えて,効率が,パラメータの分だけ徐々に圧縮されていくことを示している.したがって,パラメータaが小さいと急激にその効果が落ちることを意味している.ワイブル分布のパラメータlは,効率の初期値を表わしている.したがって,lが大きい値遡及率が高いが,aが小さいと効果が減衰していく.
ワイブル分布は,行動の測定モデルから言うと,測定値(目的変数)の度数カウントの機制(指数分布族の性質)に関する対数関数モデルと,物理量(独立変数)の心理的圧縮機制(ベキ法則,バネモデル)の2つの機制が重なっている,と言える.したがって,自然な要因空間を形成するには,対数の2重の変換(目的変数の指数モデルと独立変数のベキバランスモデル)が必要になる.
飽和する速さは,要因のウェイトとも言えるので,多変量の場合に一般化することができる.y=1-exp(-lx1a1・x2a2・・・xnan)という形になる.これは,一見,複雑そうに見えるが,ベキ効果(圧縮性や増幅性のバネモデル)が,複数の要因によって起こると考えるので,幾何平均モデルあるいは対数平均モデルであることを意味している.ワイブル分布は学習効果(単一の広告効果など)だけでなく,多要因の効果(メディアミックスなど),あるいは,多要因を前提にした初期故障率の分析などに適用することができる.(2003.3)
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献